How to prove tan3x = 3tanx tan^3x/1 3tan^2x Trigonometry Formula Proofs #Howtoprovetan3x=3tanxtan^3x/13tan^2x #TrigonometryFormulaProofs Name RANJITSin − 1 `((2x)/(1x^2))` = π 2 tan 1 x `because2tan^1x=pisin^1((2x)/(1x^2)) "for" x>1` Concept Inverse Trigonometric Functions (Simplification and Examples)One can show using simple geometry that t = tan(φ/2) The equation for the drawn line is y = (1 x)t The equation for the intersection of the line and circle is then a quadratic equation involving t The two solutions to this equation are (−1, 0) and (cos φ, sin φ)
If Sin 1 2a 1 Cos 1 1 1 Tan 1 2x 1 X2 Where A X 0 1 Then The Value Of X Is Studyrankersonline
Tan^-1(2x/1-x^2) formula
Tan^-1(2x/1-x^2) formula- 𝑑𝑥 Now we know that ∫1 〖𝑓(𝑥) 𝑔(𝑥) 〗 𝑑𝑥=𝑓(𝑥) ∫1 𝑔(𝑥) 𝑑𝑥−∫1 (𝑓′(𝑥)∫1 𝑔(𝑥) 𝑑𝑥) 𝑑𝑥 Putting f(x) = tan–1 x and g(x) = 1 (𝑈𝑠𝑖𝑛𝑔 𝑡=tan^(−1)(𝑥) ) = 2𝑥 tan^(−1) 𝑥−2∫1 𝑥/(1 𝑥^2 ) Prove that tan^1x tan^1(2x/1x^2)= tan^1(3xx^3/13x^2) asked Mar 26 in Trigonometry by Badiah (285k points) inverse trigonometric functions;




Ex 2 2 5 Simplify Tan 1 Root 1 X2 1 X Chapter 2
Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeWe've put together a list of 8 money apps to get you on the path towards a bright financial future , Engineer, interested in Basic Mathematics We know tan 2x = 2 tanx / (1 tan^2x) 2 tan^2x = 1 tan^2 x x = pi/6 {x is angle expressed in radians} General solution is x = 2* n * pi pi/6 Here is the process of my consideration Suppose $\\displaystyle \\tan\\alpha =x,\\ \\tan\\beta =\\frac{x^{2} 1}{2x}$ So the formular could be $\\displaystyle 2
2tanx 1 tan2x = 2 sinx cosx sec2x = 2 sinx cosx 1 cos2x = 2sinx cosx × cos2x 1 = 2sinxcosx = sin2x Answer linkSolution Let's use the double angle formula cos 2a = 1 − 2 sin 2 a It becomes 1 − 2 sin 2 a = sin a 2 sin 2 a sin a − 1=0, Let's factorise this quadratic equation with variable sinx (2 sin a − 1)(sin a 1) = 0 2 sin a − 1 = 0 or sin a 1 = 0 sin a = 1/2 or sin a = −1 To check other mathematical formulas and examplesTrigonometry Solve for ?
0 votes 1 answer Prove that tan^1x tan^1(2x/(1 x^2)) = tan^1((3x x^3)/(1 3x^2))Tan1 (2x/(1x 2)=2tan1 x cot1 ((1x 2)/2x 2)=tan1 (2x 2 /(1x 2)) use the formula tan1 a tan1 b =tan1 ((ab)/(1ab))6 years ago The question is ∫ tan 1 1/ (x 2 x1) dx This can be written as ∫ tan1 { (x1)x} / {1x (x1)} dx From the formula of tan1 (mn) / 1mn , We get ∫ tan1 (x1) – tan1 x dx I guess now you can proceed on your own




How To Solve Tan 1 2x 1 X2 Cot 1 1 X2 2x Pie 3 Brainly In



If Sin 1 2a 1 Cos 1 1 1 Tan 1 2x 1 X2 Where A X 0 1 Then The Value Of X Is Studyrankersonline
Tan x/2 = ±√ (1 cos x)/ (1 cos x) (algebra) Halfangle identity for tangent There are easier equations to the halfangle identity for tangent equation We will use the following trigonometric formula to prove the formula for tan 2x tan (a b) = (tan a tan b)/ (1 tan a tan b) We have tan 2x = tan (x x) = (tan x tan x)/ (1 tan x tan x) = 2 tan x/ (1 tan 2 x) Hence, we have derived the tan 2x formula using the angle sum formula of the tangent functionWe can prove the double angle identities using the sum formulas for sine andIf cos^1 x/^2 2xy/ab cos alpha y^2/b^2 = sin^2alpha Inverse Trigonometric Functions The total surface area of a




Integration Tan 1 2x 1 X2 Dx Explain In Great Detail Mathematics Topperlearning Com 4z4t9u99




Sin 1 2x 1 X 2 Formula Baldwin Cyprian
Let's see tan(AB)= (tanAtanB)/(1tanA*tanB) Now putting B=A , we get, tan(AA)= (tanAtanA)/(1tanA*tanA) tan2A= 2tanA/(1tan^2A) Hope, now it's fine we first need to know the following relationships between tantheta &cot theta we have cottheta=1/tantheta also cottheta=tan(pi/2theta) let y=tan^(1)x=>x=tany x=tany=>1/x=1/tany=coty 1/x=coty=tan(pi/2y) pi/2y=tan^(1)(1/x) but y=tan^(1)x so pi/2=tan^(1)(1/x)tan^(1)x as reqd Inverse Trigonometric Formulas Trigonometry is a part of geometry, where we learn about the relationships between angles and sides of a rightangled triangleIn Class 11 and 12 Maths syllabus, you will come across a list of trigonometry formulas, based on the functions and ratios such as, sin, cos and tanSimilarly, we have learned about inverse trigonometry concepts also




Inverse Circular Function Study Material For Iit Jee Askiitians
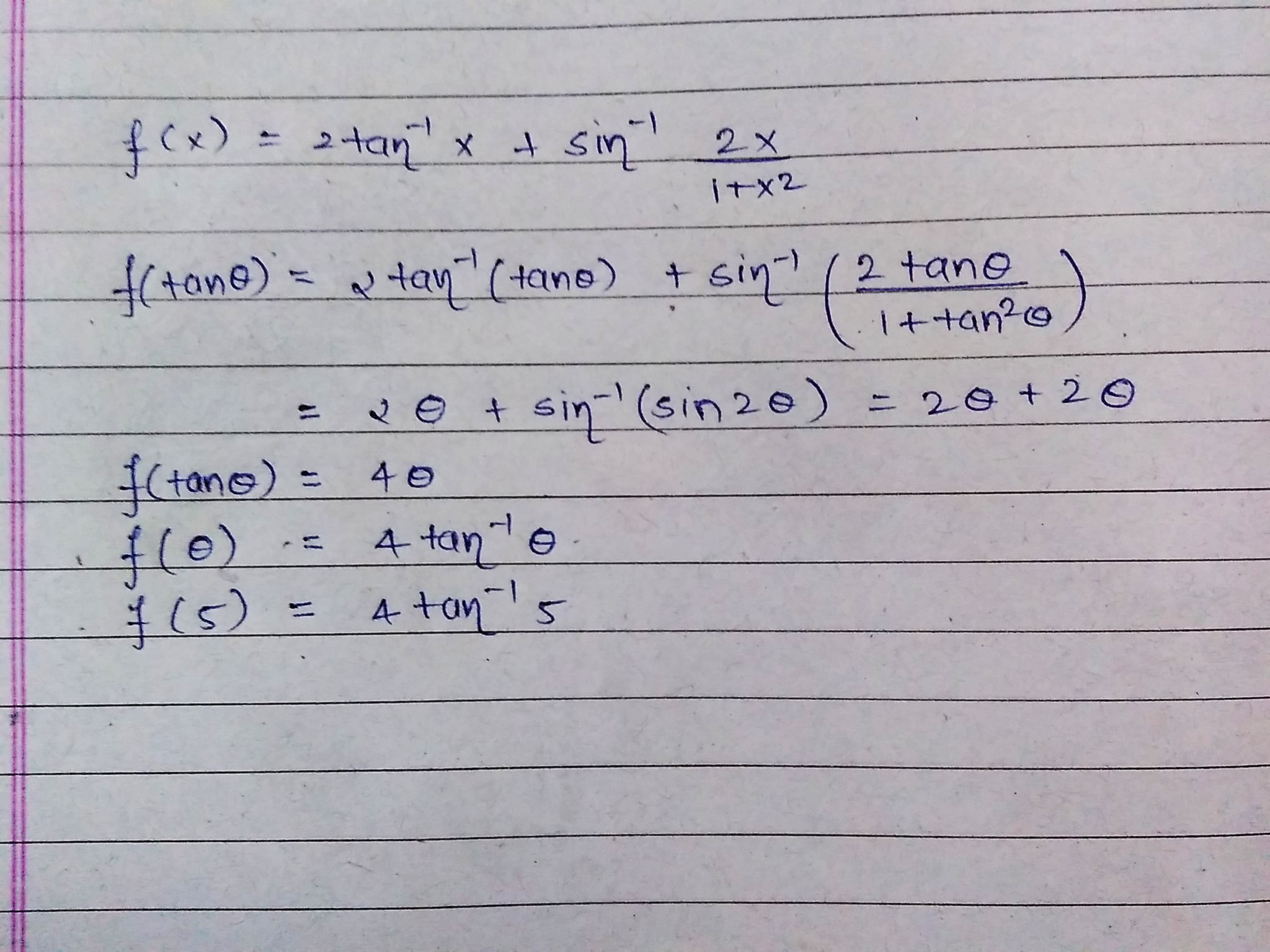



F X 2 Tan 1x Sin 1 2x 1 X 2 Then F 5
1tan^2x=sec^2x Change to sines and cosines then simplify 1tan^2x=1(sin^2x)/cos^2x =(cos^2xsin^2x)/cos^2x but cos^2xsin^2x=1 we have1tan^2x=1/cos^2x=sec^2xAnswer (1 of 3) 1sin^2x=1(1cos^2x) = 2cos^2x 1sin^2x= 2 cos^2x(1) Answer The derivative of tan^1x is 1/(1x^2) (for "why", see note below) So, applying the chain rule, we get d/dx(tan^1u) = 1/(1u^2)*(du)/dx In this question u = 2x, so we get d/dx(tan^1 2x) = 1/(1(2x)^2)*d/dx(2x) = 2/(14x^2) Note If y = tan^1x, then tany = x Differentiating implicitly gets us sec^2y dy/dx = 1," " so dy/dx = 1/sec^2y From trigonometry, we know that 1tan^2y =



Derivatives Of Inverse Trigonometric Functions Class 12 Maths Geeksforgeeks




Ex 7 6 22 Integrate Sin 1 2x 1 X 2 Teachoo Ex 7 6
This calculus video tutorial shows you how to find the derivatives if inverse trigonometric functions such as inverse sin^1 2x, tan^1 (x/2) cos^1 (x^2) ta4 Write x 25x as x^25*x 3 Use paranthesis() while performing arithmetic operations Eg1 Write sinxcosxtanx as sin(x)cos(x)tan(x) 2 Write secx*tanx as sec(x)*tan(x) 3 Write tanx/sinx as tan(x)/sin(x) 4 Use inv to specify inverse and ln to specify natural log respectively Eg1 Write sin1 x as asin(x) 2 Write ln x as ln(x) 5Tan2x = 2tanx/(1tan^2x) How!




Solve Tan 1 1 1 2x Tan 1 1 1 4x Tan 1 2 X 2




Tangent Half Angle Formula Wikipedia
Tan (2x) We know that tan x = sin x / cos x sin (2x) / cos (2x) We know that sin 2A = 2 sin A cos A 2 sin x cos x / cos (2x) Also cos 2A = cos²A – sin²A 2 sin x cos x / (cos²x – sin²x) = Divide the numerator and denominator by cos²x (2 sin x cos x / cos²x) / (cos²x – sin²x) / cos²x =Tan (x/2)=1 tan ( x 2) = 1 tan ( x 2) = 1 Take the inverse tangent of both sides of the equation to extract x x from inside the tangent x 2 = arctan(1) x 2 = arctan ( 1) The exact value of arctan(1) arctan ( 1) is π 4 π 4 x 2 = π 4 x 2 = π 4 Multiply both sides of the equation by 2 2The integration of tangent inverse is of the form I = ∫ tan – 1 x d x To solve this integration, it must have at least two functions, however it has only one function tan – 1 x So, consider the second function as 1 Now the integration becomes I = ∫ tan – 1
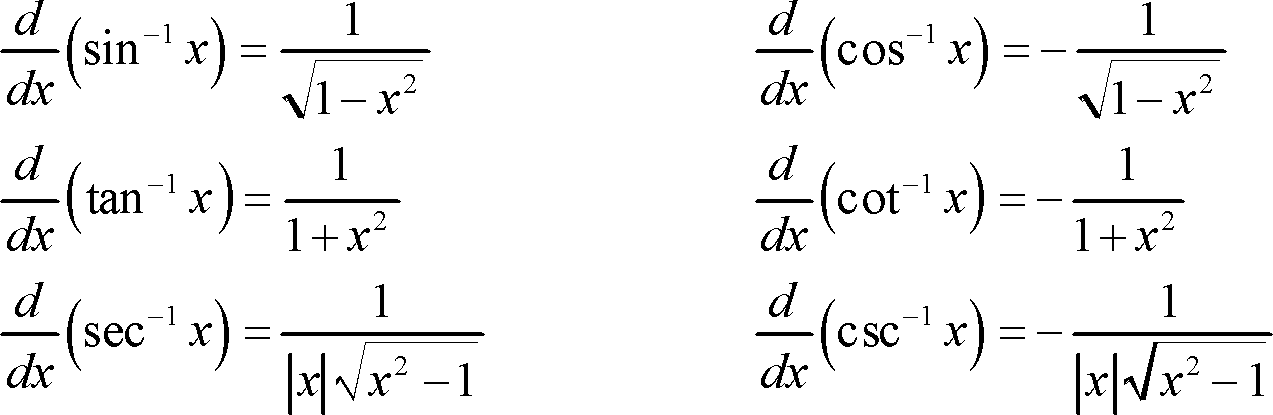



How Do You Find The Derivative Of Sin 1 2x 1 Socratic



Solve For X Tan 1 2x 1 X 2 Cot 1 1 X 2 2x P 3 1 X 1 Sarthaks Econnect Largest Online Education Community
Answer (1 of 14) This turns out to be one of the integrals that students are asked to commit to memory You can easily show that the derivative of inverse tan is 1/(1x^2) using implicit differentiation I will do that here y = tan^{1}(x) can be converted toFree derivative calculator differentiate functions with all the steps Type in any function derivative to get the solution, steps and graphAnswer (1 of 4) Let x = \tan \theta, so that \theta = \tan^{1} x, dx = \sec^2{\theta} d\theta Then the given integral is equivalent to \displaystyle \int \tan^{1



This Is Android Free Tan1 2 Sin 1 2x 1 X 2 Cos 1 1 Y 2 1 Y 2 X Y 1 Xy If X Lt 1



1
First, the constant function satisfies the property of being of degree ≤2 Next, it clearly interpolates the given dataIntroduction to Tan double angle formula let's look at trigonometric formulae also called as the double angle formulae having double angles Derive Double Angle Formulae for Tan 2 Theta \(Tan 2x =\frac{2tan x}{1tan^{2}x} \) let's recall the addition formula \(tan(ab) =\frac{ tan a tan b }{1 tan a tanb}\) So, for this let a = b , it becomesThe differentiation of the inverse tan function with respect to x is equal to the reciprocal of the sum of one and x squared d d x ( tan − 1 ( x)) = 1 1 x 2



2




Integrate Int Tan 1 2x 1 X 2 Dx
General solution of tan( 2 x) tan( x) = 1 x, and got the solution as ( 2 n 1) π 6 ( π 2 − x) So, 2 x = n π π 2 − x So, 3 x = ( 2 n 1) π 2 ( 2 x), and got the solution as ( 6 n ± 1) π 6 I can see that my solution has odd multiples of π / 2, which should be discarded, but I thought of it only after checking the solutionAnswer We must have the polynomial interpolant is P2(x) ≡1 meaning that P2(x) is the constant function Why? Misc 44 (MCQ) Chapter 7 Class 12 Integrals (Term 2) Last updated at by Teachoo Next Integration Formula Sheet Chapter 7 Class 12 Formulas→




If Y Tan 1x 2 Show That X 2 1 2y2 2x X 2 1 2




Misc 44 Mcq Value Fo Tan 1 2x 1 1 X X2 Dx Is
Proof Half Angle Formula tan (x/2) Product to Sum Formula 1 Product to Sum Formula 2 Sum to Product Formula 1 Sum to Product Formula 2 Write sin (2x)cos3x as a Sum Write cos4xcos6x as a Product Prove cos^4 (x)sin^4 (x)=cos2x Prove sinxsin (5x)/ cosxcos (5x)=tan3x To get the formula for tan 2A, you can either start with equation 50 and put B = A to get tan(A A), or use equation 59 for sin 2A / cos 2A and divide top and bottom by cos² A Either way, you get (60) tan 2A = 2 tan A / (1 − tan² A) Sine or Cosine of a Half AngleTan(x−y) = (tan x–tan y)/ (1tan x • tan y) Double Angle Identities sin(2x) = 2sin(x) • cos(x) = 2tan x/(1tan 2 x) cos(2x) = cos 2 (x)–sin 2 (x) = (1tan 2 x)/(1tan 2 x) cos(2x) = 2cos 2 (x)−1 = 1–2sin 2 (x) tan(2x) = 2tan(x)/ 1−tan 2 (x) sec (2x) = sec 2 x/(2sec 2 x) csc (2x) = (sec x csc x)/2;
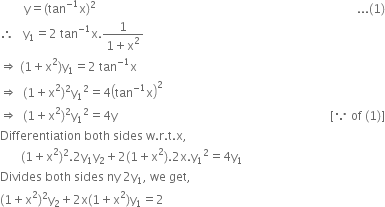



If Y Tan 1 X 2 Then Prove That 1 X2 2 Y2 2x 1 X2 Y1 2 From Mathematics Continuity And Differentiability Class 12 Up Board




If Y Tan 1 X 2 Prove That 1 X2 2y2 2x 1 X2 Y1 2 Explain In Great Detail Mathematics Topperlearning Com Z68xug
Tan (2x/1 x2) let tan1(2x/1 x2) = P tan p = 2x/1 x2 = tan2(p/2) = 2x/1 x2 2tan(p/2)/1 tan2(p/2) = 2x/1 x2 x = (tanp/2) tan1(x) = p/2 p = 2tan1x tan1 #2 tan x/(1tan^2x)=(2sin x/cos x)/(1(sin^2x/cos^2x)# #=2 sin x cos x/(cos^2xsin^2x)# #=(sin 2x)/(cos 2x)=tan 2x# Proofs for #sin 2x = 2 sin x cos x and cos 2x = 1 2 sin^2x# Use Area of a #triangle# ABC = 1/2(base)(altitude) = 1/2 bc sin A Here, it is the #triangle# ABC of a unit circle, with center at A, B and C on the circle and #(x0,1),(x1,1),(x2,1) What is the polynomial P2(x)inthiscase?
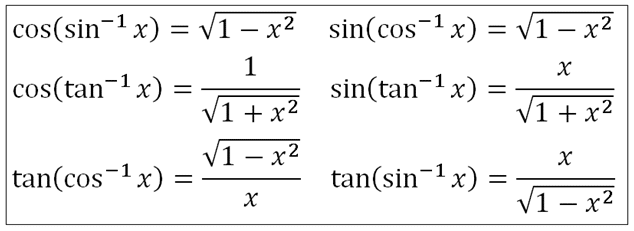



Inverse Trig Identities Reciprocal Of Trigonometric Function Trig




21 Differentiation And Integration Of Trigonometry Function 9709
Variation of lab bhattacharjee's answer $$\tan^2x=\tan(xa)·\tan(xb) \Rightarrow \\ \tan^2x1=\tan(xa)·\tan(xb)1 \Rightarrow \\ \frac{1}{\cos^2 x}=\tan(xa)·\tan(xb)1 \Rightarrow \\ \cos^2x =\frac1{\tan(xa)·\tan(xb)1} \Rightarrow \\ \frac{1\cos 2x}{2}=\frac1{\tan(xa)·\tan(xb)1} \Rightarrow \\\\ \cos 2x=\frac2{\tan(xa)·\tan(xb)1}1 Misc 14 Solve tan1 (1 − x)/(1 x) = 1/2 tan1 x, (x > 0) tan1 (1 − x)/(1 x) = 1/2 tan1 x 2 tan1 ((1 − x)/(1 x)) = tan1 x tan1 (2 ((1 − 𝑥)/(1Free online tangent calculator tan(x) calculator This website uses cookies to improve your experience, analyze traffic and display ads




Rewrite Sin Cos 1 X Tan 1 Y As An Algebraic Function Of X And Y Mathematics Stack Exchange




Tan 1 X 1 X 2 Dx Evaluate The Indefinite Integral Youtube
The derivative of tan 2x is 2 sec 2 (2x) The integral of tan 2x is (1/2) ln cos 2x C or (1/2) ln sec 2x C Topics Related to Tan 2x Tangent Formulas;Solve for x tan (2x)=1 tan (2x) = 1 tan ( 2 x) = 1 Take the inverse tangent of both sides of the equation to extract x x from inside the tangent 2x = arctan(1) 2 x = arctan ( 1) The exact value of arctan(1) arctan ( 1) is π 4 π 4 2x = π 4 2 x = π 4 Divide each term byThe inverse function reverses this operation, taking the ratio of sides as input and returning the angle as output sin − 1 ( b c) = θ cos − 1 ( a c) = θ tan − 1 ( b a) = θ = θ = θ = θ This means the inverse trigonometric functions are useful whenever we




How Do You Find The Equations Of The Tangent Lines To The Curve Y X 1 X 1 That Are Parallel To The Line X 2y 2 Socratic



Considering The Principal Solutions Find The Number Of Solutions Of Tan 1 2x Tan 1 3x Pie 4 Mathematics Topperlearning Com 7437
Hence the integral of tan 2x is given by (1/2) ln cos 2x C or (1/2) ln sec 2x C Important Notes on Tan 2x Formula tan 2x = 2tan x / (1 − tan 2 x) tan 2x = sin 2x/cos 2x;




Ex 2 2 15 If Tan 1 X 1 X 2 Tan 1 X 1 X 2 Pi 4



1
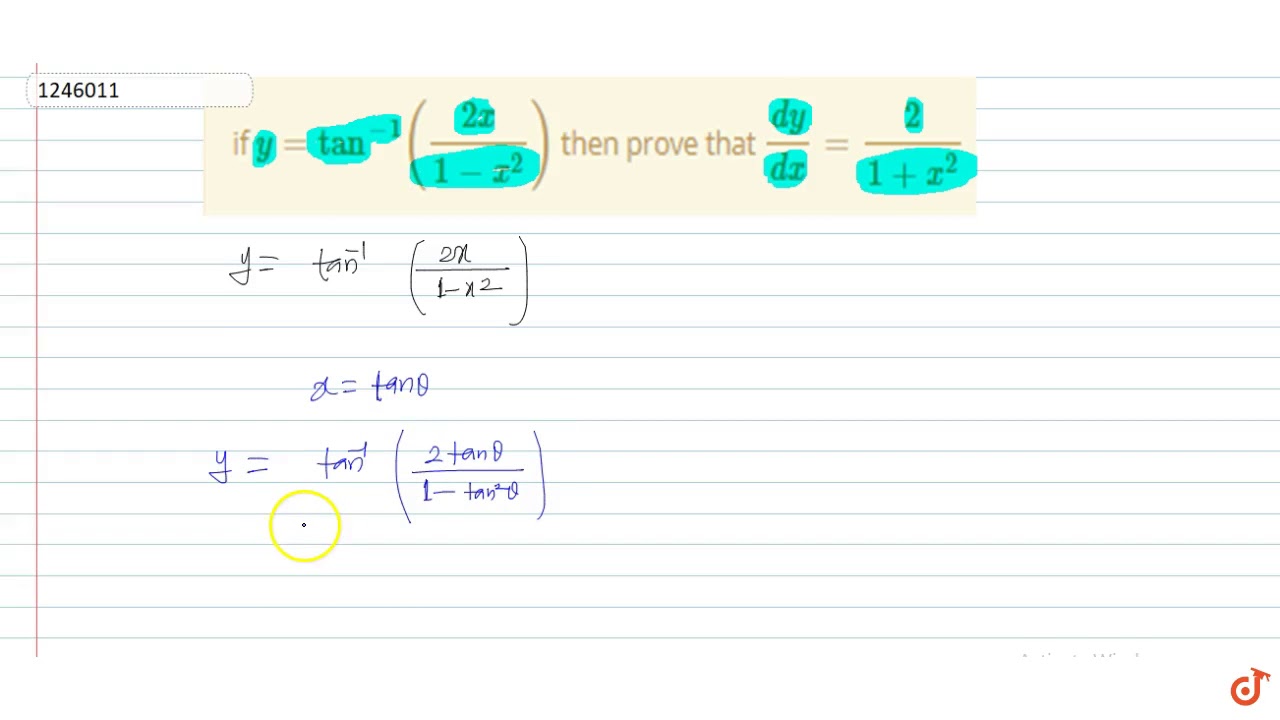



If Y Tan 1 2x 1 X 2 Then Prove That Dy Dx 2 1 X 2 Youtube




Derivative Of Tan Inverse X Formula What Is Derivative Of Arctan



1




Prove That 2tan 1x Tan 1 2x 1 X 2 Maths Inverse Trigonometric Functions Meritnation Com




Solved 1 8 Find The Exact Value Of Each Expression 1 A Chegg Com



If 3 Tan 1 X Cot 1 X P Then X Equals Studyrankersonline




If Y Tan 1 1 1 X X 2 Tan 1 1 X 2 3x 3 Tan 1 1 X 2 5x 7 Upto N Terms Then Fin Youtube



Prove That 2tan 1x Tan 2x 1 X 2 Brainly In
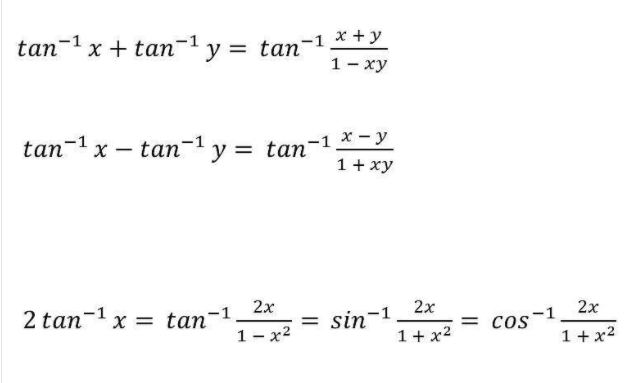



Formula Of Trigonometry Sin Cos Tan Cot Sec Cosec




Ex 2 2 5 Simplify Tan 1 Root 1 X2 1 X Chapter 2




Ex 7 6 22 Integrate Sin 1 2x 1 X 2 Teachoo Ex 7 6




Example 13 Solve Tan 1 2x Tan 1 3x Pi 4 Class 12




Inverse Trigonometric Functions Xii 1



What Is The Value Of Dy Dx If Y Tan 1 4 X 1 4x Quora



Show That Cos 2 Tan 1 1 7 Sin 4 Tan 1 1 3 Studyrankersonline




1 Tan 2x 1 Tan 2 X 1 2cos 2 X Youtube




Solve Tan 1 X Tan 1 2x 1 X 2 Pi 3




Inverse Trigonometric Functions Class 12 Notes Maths Chapter 2 Learn Cbse Class12mathsnotes Inver Trigonometric Functions Math Formula Chart Class 12 Maths




Answered Use Power Series Operations To Find The Bartleby
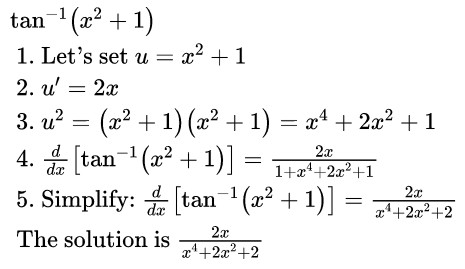



Derivative Of Arctan X Inverse Tangent Detailed Lesson
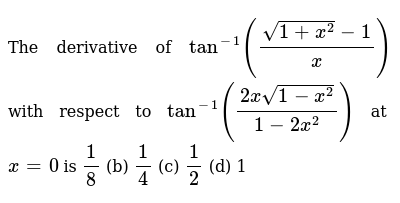



The Derivative Of Tan 1 Sqrt 1 X 2 1 X With Respect To Tan 1 2xsqrt 1 X 2 1 2x 2 At X 0 Is 1 8 B 1 4 C 1 2 D 1




Ex 2 2 13 Inverse Trigonometry Tan 1 2 Sin 1 2x 1 X2



Inverse Trigonometric Functions Xii 1




Misc 44 Mcq Value Fo Tan 1 2x 1 1 X X2 Dx Is




Wolfram Alpha Examples Step By Step Solutions




Worked Example Implicit Differentiation Video Khan Academy




Prove That Tan Inverse X Tan Inverse 2x 1 X Square Tan Inverse 3x X Cube 1 3x Square X Maths Inverse Trigonometric Functions Meritnation Com




Tan2x 1 ただの悪魔の画像




Math Backup Posts Facebook




Inverse Circular Function Study Material For Iit Jee Askiitians




Tangent Half Angle Formula Wikipedia




If Y Tan 1 X 2 Then Prove That 1 X 2 2 Y 2 2x 1 X 2 Y 1 2




Derivatives Of Inverse Trigonometric Functions Sin 1 2x Cos 1 X 2 Tan 1 X 2 Sec 1 1 X 2 Youtube




Inverse Circular Function Study Material For Iit Jee Askiitians



Inverse Trigonometric Functions Precalculus Ii




Drill Find Dy Dx Y X 3 Sin 2x Y E 2x Ln 3x 1 Y Tan 1 2x Product Rule X 3 2cos 2x 3x 2 Sin



Differentiate Tan 1 1 X 2 X With Respect To Cos 1 2x 1 X 2 When X 0 Sarthaks Econnect Largest Online Education Community




Sin 1 2x 1 X 2 Formula Baldwin Cyprian



How To Evaluate Tan 2 Tan 1 1 5 Pi By 4 Quora



Tan 1 X Tan 1 Y Tan 1 X Y 1 Xy Arctan X Arctan Y Arctan X Y 1 Xy Youtube



Tan 2 Tan 1 X Tan 2 Arctan X Youtube



2



What Is The Integration Of Cot 1 1 X X 2 Dx Limits From 1 To 0 Quora




Tan Inverse 2x 1 X Square Cot Inverse 1 X Square 2x 2pi 3 Brainly In




Solve Tan 1 2x Tan 1 3x Pi 4 Youtube




Calculus I Exam 1 Spring 03 Answers
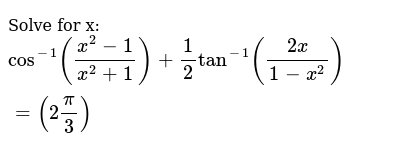



Solve For X Cos 1 X 2 1 X 2 1 1 2tan 1 2x 1 X 2
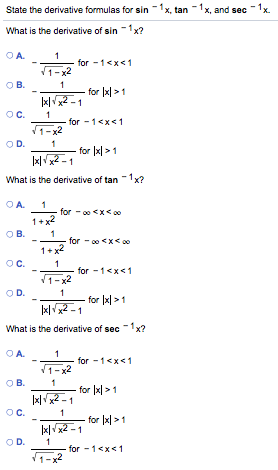



Solved State The Derivative Formulas For Sin 1 X Tan 1 X Chegg Com




Ex 7 6 22 Integrate Sin 1 2x 1 X 2 Teachoo Ex 7 6



How To Differentiate Y Tan 1 2x 1 X 2 For The Inverse Trigonometric Function Quora



Prove That I Tan 1 1 X 2 2x Cot 1 1 X 2 2x P 2 Ii Sin Tan 1 1 X 2 2x Cos 1 Sarthaks Econnect Largest Online Education Community



What Is The Nth Derivative Of Tan 1 2x 1 X 2 Quora




How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic
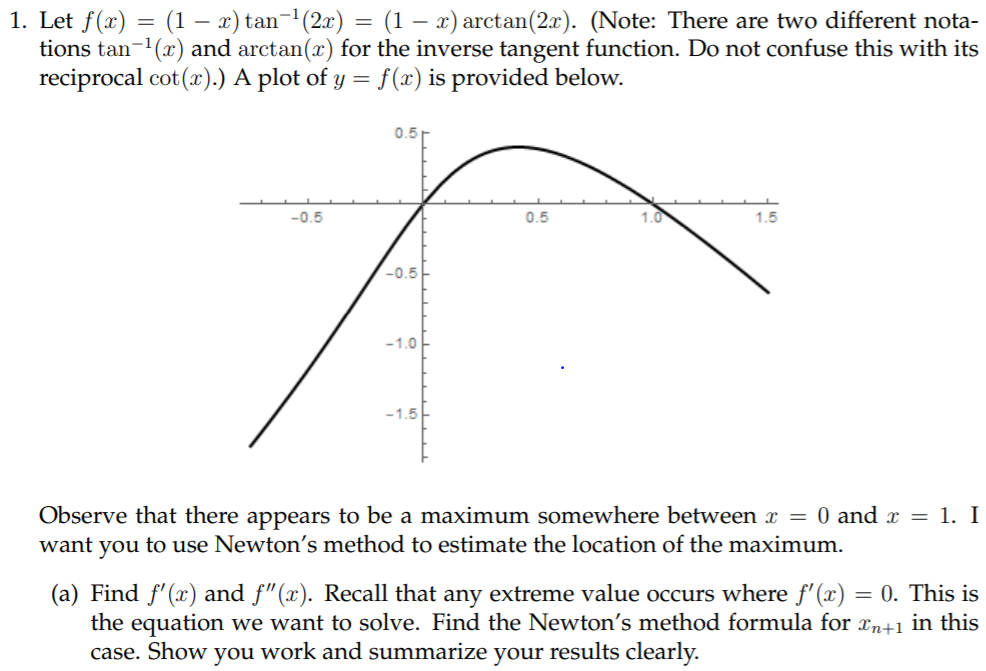



Solved 1 Let F X 1 X Tan 2x 1 X Arctan 2x Chegg Com




Prove That Tan 1x Tan 1 2x1 X 2 Tan 1 3x X 31 3x 2




Solved 8 Find The Formula For Sin 2 Tan 1 X A 1 Root 1 Chegg Com



Prove Sin2x 2tanx 1 Tan 2x Socratic



What Is Cos Tan 1 X Quora



Evaluate The Integral Sin 1 2x 1 X 2 Dx For X 0 1 Sarthaks Econnect Largest Online Education Community



2



Derivative Of Inverse Tangent




Ex 5 3 10 Find Dy Dx In Y Tan 1 3x X3 1 3x2 Ex 5 3




Compute F A Algebraically For The Given Value Of A Hint See Example 1 F X Homeworklib



2



Let Tan 1 Y Tan 1 X Tan 1 2x 1 X 2 Where X 1 3 Then A Value Of Y Is Sarthaks Econnect Largest Online Education Community




Exam 2 Review Sheet Spring 07 Calculus Ii Math 230 Docsity
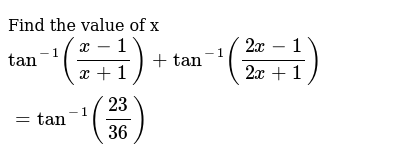



Find The Value Of X Tan 1 X 1 X 1 Tan 1 2x 1 2x 1 Tan 1 23 36



Solve The Following For X Cos 1 X 2 1 X 2 1 Tan 1 2x X 2 1 2p 3 Sarthaks Econnect Largest Online Education Community




Example 7 Show That Tan 1 X Tan 1 2x 1 X2 Inverse



1




Solved Find The Inverse Function For F X 2x 1 2x 5 Chegg Com
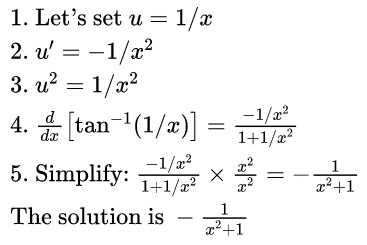



Derivative Of Arctan X Inverse Tangent Detailed Lesson



How To Find The Nth Derivative Of Math Tan 1 X Math Quora



Solve For X Tan 1 X 1 X 1 Tan 1 2x 1 2x 1 Tan 1 23 36 Sarthaks Econnect Largest Online Education Community




Evaluate Inttan 1 X Dx



Math Scene Derivatives Lesson 2 Differentiating Polynomials



0 件のコメント:
コメントを投稿